There are two possibilities: either I’m crazy, or everyone else is wrong.
Well, I’m ’bout to prove I’m not wrong.
Yes, I know it’s hard for people to accept we should abandon the standard stats curriculum in favor of the GLM.
But you can’t deny you’ll get identical results doing a t-test as a GLM.
“Prove it!,” you say?
Well, I am happy to oblige.
Let’s go ahead and run a regular old t-test:
require(flexplot)
data(avengers)
t.test(ptsd~north_south, data=avengers, var.equal=TRUE)
## ## Welch Two Sample t-test ## ## data: ptsd by north_south ## t = -8.195, df = 810, p-value = 9.755e-16 ## alternative hypothesis: true difference in means is not equal to 0 ## 95 percent confidence interval: ## -0.4112410 -0.2523058 ## sample estimates: ## mean in group north mean in group south ## 3.834729 4.166502
(Note the default t-test in R, Welch’s, does a correction which will make it not equal to a regression, hence the var.equal=TRUE. Thanks for the reminder Michael!)
Now let’s do the same thing as a glm:
mod = lm(ptsd~north_south, data=avengers)
summary(mod)
## ## Call: ## lm(formula = ptsd ~ north_south, data = avengers) ## ## Residuals: ## Min 1Q Median 3Q Max ## -2.0347 -0.3665 -0.0347 0.3653 3.2335 ## ## Coefficients: ## Estimate Std. Error t value Pr(>|t|) ## (Intercept) 3.83473 0.02863 133.954 < 2e-16 *** ## north_southsouth 0.33177 0.04048 8.195 9.76e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## Residual standard error: 0.5768 on 810 degrees of freedom ## Multiple R-squared: 0.07656, Adjusted R-squared: 0.07542 ## F-statistic: 67.16 on 1 and 810 DF, p-value: 9.755e-16
Oh, would you look at that. The t-statistic for the t-test (-8.195) is exactly the same as the t-statistic for the “slope” in the linear model (8.195), at least in absolute value. (The t-test version subtracts north from south, while the glm version does the opposite).
It’s. The. Same. Thing.
Bazinga.
Except the GLM approach gives you more than the t-test and is easily expandable; the t-test is NOT.
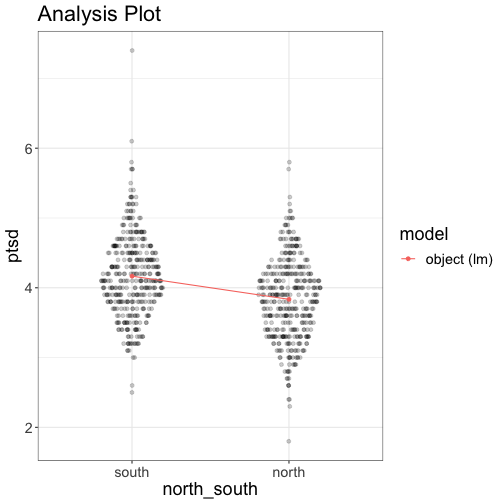
And, of course, we might as well look at a graphic of the glm (which you cannot do with the t-test, btw).
visualize(mod, plot="model")